Tag: Panduan Lengkap Menghitung Luas Permukaan Tabung

Panduan Lengkap Menghitung Luas Permukaan Tabung dengan Rumus Praktis

admin 0 Komentar Pendidikan
Panduan Lengkap Menghitung Luas Permukaan Tabung

Panduan Lengkap Menghitung Luas Permukaan Tabung dengan Rumus Praktis – Mengapa Penting Memahami Konsep Luas Permukaan Tabung? Tabung merupakan salah satu bentuk geometri yang sering kita temui dalam kehidupan sehari-hari, baik dalam desain, konstruksi, maupun benda-benda sehari-hari seperti kaleng, pipa, dan drum. Memahami cara menghitung luas permukaan tabung sangat penting, baik untuk kepentingan akademik nexus koi gate maupun aplikasi praktis di berbagai bidang. Artikel ini akan menguraikan secara lengkap langkah-langkah menghitung luas permukaan tabung menggunakan rumus matematika yang mudah dipahami.

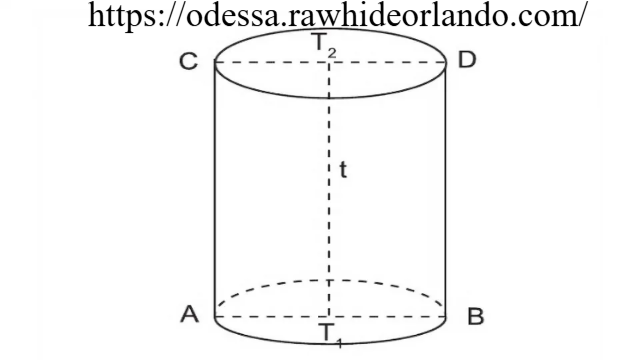
Definisi dan Karakteristik Tabung Tabung adalah bangun ruang yang memiliki dua sisi berbentuk lingkaran sebagai alas dan tutup, serta sebuah sisi lengkung yang menghubungkan kedua lingkaran tersebut. Dalam geometri, tabung memiliki tiga elemen utama:

  1. Jari-jari (r): Jarak dari pusat lingkaran ke titik pada tepinya.
  2. Tinggi (t): Jarak vertikal antara alas dan tutup tabung.
  3. Diameter (d): Dua kali jari-jari lingkaran (d = 2r).

Rumus Luas Permukaan Tabung

Luas permukaan tabung terdiri dari dua bagian:

  1. Luas sisi alas dan tutup (2 lingkaran).
  2. Luas sisi lengkung tabung.

Rumus untuk menghitung luas permukaan tabung adalah:

L=2πr2+2πrtL = 2 \pi r^2 + 2 \pi r t

Di mana:

  • π\pi (pi) adalah konstanta dengan nilai sekitar 3,14159.
  • rr adalah jari-jari alas tabung.
  • tt adalah tinggi tabung.

Langkah-langkah Menghitung Luas Permukaan Tabung

  1. Hitung Luas Alas dan Tutup Untuk menghitung luas sweet bonanza kedua lingkaran (alas dan tutup), gunakan rumus:
Luas alas dan tutup=2πr2Luas\ alas\ dan\ tutup = 2 \pi r^2
  1. Hitung Luas Sisi Lengkung Luas sisi lengkung dapat dihitung menggunakan rumus:
Luas sisi lengkung=2πrtLuas\ sisi\ lengkung = 2 \pi r t
  1. Jumlahkan Kedua Luas Gabungkan hasil dari luas alas dan tutup serta luas sisi lengkung untuk mendapatkan total luas permukaan tabung:
L=2πr2+2πrtL = 2 \pi r^2 + 2 \pi r t

Contoh Soal dan Penyelesaian Soal: Sebuah tabung memiliki jari-jari alas 7 cm dan tinggi 20 cm. Hitunglah luas permukaan tabung.

Penyelesaian: Langkah 1: Hitung luas alas dan tutup.

2πr2=2×3,14×72=2×3,14×49=307,72 cm22 \pi r^2 = 2 \times 3,14 \times 7^2 = 2 \times 3,14 \times 49 = 307,72 \ \text{cm}^2

Langkah 2: Hitung luas sisi lengkung.

2πrt=2×3,14×7×20=879,2 cm22 \pi r t = 2 \times 3,14 \times 7 \times 20 = 879,2 \ \text{cm}^2

Langkah 3: Hitung total luas permukaan.

L=307,72+879,2=1.186,92 cm2L = 307,72 + 879,2 = 1.186,92 \ \text{cm}^2

Jadi, luas permukaan tabung adalah 1.186,92 cm².

Aplikasi Praktis dari Perhitungan Luas Permukaan Tabung

  1. Desain dan Konstruksi: Menentukan jumlah material yang dibutuhkan untuk membuat benda berbentuk tabung seperti pipa atau tangki.
  2. Industri: Menghitung kapasitas pelapisan permukaan dalam proses manufaktur.
  3. Pendidikan: Konsep ini sering digunakan dalam pelajaran matematika dan fisika.

Tips Penting dalam Menghitung Luas Permukaan Tabung

  1. Gunakan nilai π\pi yang sesuai: Untuk keperluan sehari-hari, gunakan π=3,14\pi = 3,14 atau nilai lebih presisi jika diperlukan.
  2. Pastikan satuan konsisten: Jika jari-jari dalam cm, tinggi juga harus dalam cm.
  3. Periksa hasil hitungan: Lakukan pengecekan ulang untuk memastikan hasil akhir akurat.

Kesimpulan

Menghitung luas permukaan tabung dengan rumus yang tepat adalah keterampilan yang bermanfaat, tidak hanya dalam dunia pendidikan tetapi juga dalam berbagai aplikasi kehidupan nyata. Dengan mengikuti langkah-langkah dan tips di atas, Anda dapat menyelesaikan masalah geometri ini dengan mudah dan efisien. Semoga panduan ini membantu Anda memahami konsep secara menyeluruh!a